Sainte-Laguë/Schepers
The German physician Hans Schepers, at the time Head of the Data Processing Group of the German Bundestag, in 1980 suggested that the distribution of seats according to d’Hondt be modified to avoid putting smaller parties at a disadvantage. By a different calculation method, the procedure proposed by Schepers arrives at the same results as the method developed by the French mathematician André Sainte-Laguë in 1912.
The procedure according to Sainte-Laguë/Schepers has been used since 1980 for the distribution of seats in the committees and bodies of the German Bundestag. Since 2009, it is the procedure used to distribute the seats in Bundestag and European elections. It has been employed in the elections to the Länder parliaments of Bremen (since 2003), Hamburg (since 2008), Nordrhein-Westfalen (since 2010), Baden-Württemberg and Rheinland-Pfalz (since 2011), Schleswig-Holstein (since 2012), Bayern (since 2022) and Sachsen (since 2023).
In this procedure, which is also called divisor method with standard rounding, the respective numbers of second votes cast for the individual parties are divided by a joint divisor. The resulting quotients are rounded according to standard practice to obtain numbers of seats, i.e. the figure is rounded up or down when the remaining fraction is larger or smaller than 0.5, where the residual equals 0.5 exactly, a lot will be drawn. The divisor is determined in a way which ensures that the total of the numbers of seats equals the total of the seats to be distributed. Three different methods may be used for the calculation which produce the same result and thus are regarded as equal from the legal perspective:
- Highest average method: this method follows the train of thought on which the procedure according to d’Hondt is based, with the respective number of votes being divided by 0.5, 1.5, 2.5 etc. and the seats, in turn, being successively allocated by descending maximum numbers. The calculation according to d’Hondt is based on the full entitlement to a seat and therefore uses whole numbers for division, with smaller parties obtaining their first and further seats disproportionately late. In comparison, the requirements for a seat to be assigned have been lowered with this procedure. Once there is an entitlement to more than half a seat, it is already allocated.
- Rank order statistic procedure: here, the inverse values are considered instead of the maximum numbers and the seats are successively assigned according to these ascending rank order statistics.
- Iterative procedure: with this method, an approximate allocation is calculated in a first step. The total number of votes to be considered is divided by the total number of seats to be distributed, thus determining a provisional divisor for allocation. Any remaining discrepancies are reduced in the following steps by increasing or reducing the divisor until the final allocation has been found where the distribution of seats corresponds with the number of seats to be distributed.
For the distribution of seats in the elections to the German Bundestag, the legislator selected the last-mentioned iterative procedure when the procedure according to Sainte-Laguë/Schepers was introduced. For the above example, the distribution of seats would be calculated as follows:
Procedure in accordance to Section 6 (2) of the Federal Elections Act with divisor for allocation
Formula:
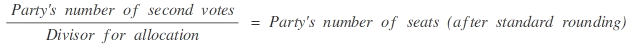
Determining the divisor for allocation (Criterion: allocation of as many seats to Land lists as there are seats to be distributed):
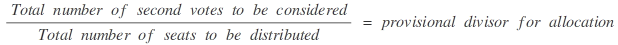
If necessary, increasing or reducing the divisor for allocation until the total calculated corresponds to the total of the seats to be distributed.
Total number of seats minus the seats obtained by successful individual candidates (constituency nomination pursuant to Section 20 (3) of the Federal Elections Act) or successful party candidates, where the party has obtained less than five percent of the valid second votes and fewer than three direct seats or has not been admitted with a Land list in the respective Land (Section 6 (2) sentence 6 in conjunction with Section 6 (1) sentence 3 of the Federal Elections Act).
Example: Allocation of 8 seats
1st step:
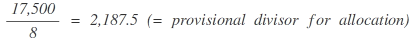
| Party | Calculation | Result after standard rounding = seats to be distributed accordingly |
|---|---|---|
| A |  |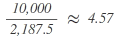
5 |
| B |  |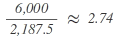
3 |
| C |  |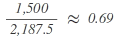
1 |
As a total of 9 seats is attributable to the parties when using the divisor 2,187.5 for allocation purposes while there are only 8 seats to be distributed, the divisor has to be increased until the calculation of the allocation of seats sums up to the number of seats to be distributed. To this end, the calculation is repeated with the higher divisor of 2,300:
2nd step:
| Party | Calculation | Results after standard rounding = seats to be distributed accordingly |
|---|---|---|
| A |  |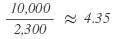
4 |
| B |  |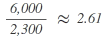
3 |
| C |  |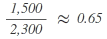
1 |
The procedure according to Sainte-Laguë/Schepers eliminates paradoxes that may occur when seats are distributed according to the Hare/Niemeyer method.
Last update: 11 July 2024